連続した面の生成
- Metasequoia > Metasequoia Python
- by yuichirou yokomakura
- 2010.08.26 Thursday 21:58
メタセコイアPython API面白いです。
CGの基礎となる原理を理解するのに役立ちます。
二つの面をリストを設けて、そのつどaddFace()していると、面はばらばらでつながっていません。頂点が共有されていないです。
そこで、下記のようなモデルをつくり、Obj出力してみました。
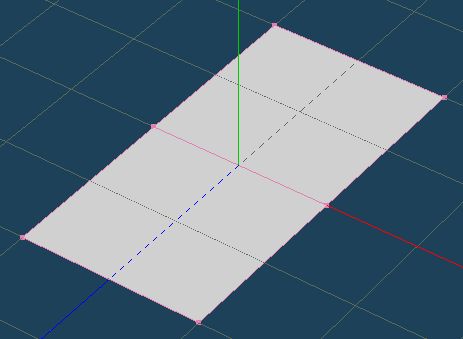
頂点情報と面の情報が書かれています。
これを参考にしてMetasequoia Pythonで書いてみることにしました。
addFace()の中は
obj.addFace([a1,a2,a3,a4])
obj.addFace([a3,a5,a6,a4])
と書いてもリストで頂点のインデックス番号でもOKなんですね。
obj.addFace([0,1,2,3])
obj.addFace([2,5,4,3])
リストの中の順番が重要です。反時計回りに並んでます。
この番号は、以下のa5からa1まで順に記述した番号を0から5までを割り当てています。だから以下のa5をコメントアウトすると、次行のa6が0番になります。
以下、サンプルファイルです。実験君ですね。ありがとうございます。
CGの基礎となる原理を理解するのに役立ちます。
二つの面をリストを設けて、そのつどaddFace()していると、面はばらばらでつながっていません。頂点が共有されていないです。
そこで、下記のようなモデルをつくり、Obj出力してみました。

# Created by Metasequoia
v 50.000000 0.000000 100.000000
v -50.000000 0.000000 100.000000
v -50.000000 0.000000 0.000000
v 50.000000 0.000000 0.000000
v -50.000000 0.000000 -100.000000
v 50.000000 0.000000 -100.000000
# 6 vertices
f 4 3 2 1
f 4 6 5 3
# 2 elements
頂点情報と面の情報が書かれています。
これを参考にしてMetasequoia Pythonで書いてみることにしました。
addFace()の中は
obj.addFace([a1,a2,a3,a4])
obj.addFace([a3,a5,a6,a4])
と書いてもリストで頂点のインデックス番号でもOKなんですね。
obj.addFace([0,1,2,3])
obj.addFace([2,5,4,3])
リストの中の順番が重要です。反時計回りに並んでます。
この番号は、以下のa5からa1まで順に記述した番号を0から5までを割り当てています。だから以下のa5をコメントアウトすると、次行のa6が0番になります。
以下、サンプルファイルです。実験君ですね。ありがとうございます。
# 基本図形、新規オブジェクトで平面をつくる
#meta_4men2.py
doc = MQSystem.getDocument()
obj = MQSystem.newObject() #新規オブジェクト
out = MQSystem.println
out(obj.name)
a=doc.getObjectIndex(obj) #オブジェクトのインデックスを取得
obj.name="plane_%d" % a #オブジェクト名をつける
a5=obj.addVertex(-50.000000,0.000000,-100.000000) #0
a6=obj.addVertex(50.000000,0.000000,-100.000000) #1
a4=obj.addVertex(50.000000,0.000000,0.000000) #2
a3=obj.addVertex(-50.000000,0.000000,0.000000) #3
a2=obj.addVertex(-50.000000,0.000000,100.000000) #4
a1=obj.addVertex(50.000000,0.000000,100.000000) #5
#obj.addFace([a1,a2,a3,a4])
#obj.addFace([a3,a5,a6,a4])
obj.addFace([0,1,2,3])
obj.addFace([2,5,4,3])
doc.addObject( obj )
num = doc.numObject #オブジェクトの数
out("オブジェクトの数 %d" % num) #オブジェクトの数を表示
#obj.deleteFace(1)- -
- -