<< ポリゴン面の求め方 python cgkitを利用 戻る 面法線と頂点法線　その2　RIB出力 >>

面法線と頂点法線

前回の記事のリンク先を参考に、頂点法線を求めてみた。とんでもなく面倒だけど、考え方がちょっとわかりました。

以下は、cgkitを利用してベクトルを求め、外積、そして正規化を行った。
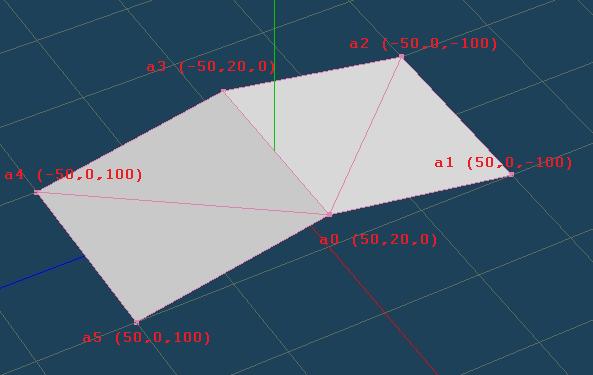
メタセコイアでモデルを作り、各頂点の法線をRIBエクスポートするPolyconv(cnv)やmtrで出してみた。
normal01.jpg

C:\Python26>python
Python 2.6.4 (r264:75708, Oct 26 2009, 08:23:19) [MSC v.1500 32 bit (Intel)] on
win32
Type "help", "copyright", "credits" or "license" for more information.

cgkit起動

>>> from cgkit.all import *


頂点座標を入力
>>> a0=vec3(50,20,0)
>>> a1=vec3(50,0,-100)
>>> a2=vec3(-50,0,-100)
>>> a3=vec3(-50,20,0)
>>> a4=vec3(-50,0,100)
>>> a5=vec3(50,0,100)

----------------------------
a1の頂点法線を求める
ベクトル算出
>>> v1=a0-a1
>>> v2=a2-a1
外積　反時計回り
>>> n0=v2.cross(v1)
a1の頂点法線
>>> a1n=n0.normalize()
>>> a1n
(0, 0.980581, -0.196116)

-----------------------------
a2の頂点法線を求める
>>> v1=a1-a2
>>> v2=a0-a2
外積　反時計回り
>>> n0=v2.cross(v1)

>>> v1=a0-a2
>>> v2=a3-a2
外積　反時計回り
>>> n1=v2.cross(v1)
>>> n0
(0, 10000, -2000)
>>> n1
(0, 10000, -2000)

各法線を加える
>>> n2=n0+n1
正規化する
>>> a2n=n2.normalize()
a2の頂点法線
>>> a2n
(0, 0.980581, -0.196116)

-------------------------------
a3の頂点法線を求める
>>> v1=a2-a3
>>> v2=a0-a3
>>> n0=v2.cross(v1)
>>> n0
(0, 10000, -2000)
>>> v1=a0-a3
>>> v2=a4-a3
>>> n1=v2.cross(v1)
>>> n1
(-0, 10000, 2000)

各法線を加える
>>> n2=n0+n1
>>> n2
(0, 20000, 0)
正規化する
>>> a3n=n2.normalize()
a3の頂点法線
>>> a3n
(0, 1, 0)

----------------------------
a4の頂点法線を求める
>>> v1=a3-a4
>>> v2=a0-a4
>>> n0=v2.cross(v1)
>>> n0
(0, 10000, 2000)

>>> v2=a5-a4
>>> v1=a0-a4
>>> n1=v2.cross(v1)
>>> n1
(-0, 10000, 2000)

各法線を加える
>>> n2=n0+n1
正規化する
>>> a4n=n2.normalize()

a4の頂点法線
>>> a4n
(0, 0.980581, 0.196116)

----------------------------
a5の頂点法線を求める
>>> v2=a0-a5
>>> v1=a4-a5
>>> n0=v2.cross(v1)
>>> n0
(0, 10000, 2000)
正規化する
>>> a5n=n0.normalize()

a5の頂点法線
>>> a5n
(0, 0.980581, 0.196116)
-----------------------------
a0の頂点法線を求める
>>> v2=a4-a0
>>> v1=a5-a0
>>> n0=v2.cross(v1)
>>> n0
(0, 10000, 2000)
>>> v2=a3-a0
>>> v1=a4-a0
>>> n1=v2.cross(v1)
>>> n1
(0, 10000, 2000)
>>> v2=a2-a0
>>> v1=a3-a0
>>> n2=v2.cross(v1)
>>> n2
(0, 10000, -2000)
>>> v2=a1-a0
>>> v1=a2-a0
>>> n3=v2.cross(v1)
>>> n3
(0, 10000, -2000)

各法線を加える
>>> nn=n0+n1+n2+n3
正規化する
>>> a0n=nn.normalize()

a0の頂点法線
>>> a0n
(0, 1, 0)
  • -
  • -

<< ポリゴン面の求め方 python cgkitを利用 戻る 面法線と頂点法線　その2　RIB出力 >>