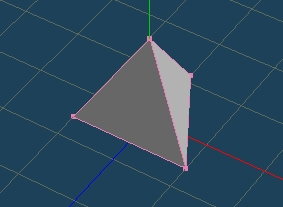
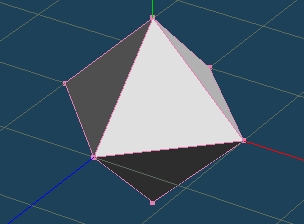
メタセコイアPython 円柱をつくる その2
- Metasequoia > Metasequoia Python
- by yuichirou yokomakura
- 2010.09.03 Friday 00:18
円柱に上下、ふたをしてみた。点の順番で苦労した。面倒ですが、できるとうれしい。Y方向に配置しました。試してみるのが一番、Metasequoia Pythonコツコツやっていきます。使い方、探究心、広がります。ありがとうございます。
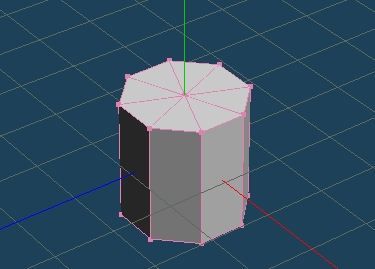

import math
def p(*args):
"""
プリント関数
複数の引数を渡せる。
"""
if len(args)==0:
# 改行させる
MQSystem.println("")
return
for arg in args:
MQSystem.println(str(arg))
#drawCyl2.py
doc = MQSystem.getDocument()
out = MQSystem.println
def drawCylinder(Nxy,r=50):
obj = MQSystem.newObject()
s=MQSystem.newPoint
#直径50、高さ50の円柱(中心が原点),分割数:Nxy
PI=3.1415926535
if Nxy>16:
Nxy = 16
p={} #dictionary
theta0 = PI/Nxy
for i in range(Nxy):
theta = -theta0+2.0*theta0*i
p[i] = s(r*math.cos(theta),r, r*math.sin(theta)) #上底のx成分,y成分(高さ),z成分
p[i+Nxy] = s(r*math.cos(theta), -r, r*math.sin(theta)) #下底のx成分,y成分,z成分
#上底
for i in range(Nxy):
out(str(i))
obj.addVertex(p[i])
obj.addVertex( MQSystem.newPoint( 0.0, r, 0.0 ) )
for i in range(Nxy):
obj.addFace([(i+1)%Nxy,Nxy,i])
#下底
for i in range(Nxy,2*Nxy):
out("v"+str(i))
obj.addVertex(p[i])
obj.addVertex( MQSystem.newPoint( 0.0, -r, 0.0 ) )
for i in range(Nxy,2*Nxy):
if i+2==Nxy*2+1:
obj.addFace([i+1,Nxy*2+1,Nxy+1])
out(str(i+1))
else:
obj.addFace([i+1,Nxy*2+1,i+2])
out("e"+str(i+1))
#側面
for i in range(Nxy):
ii = i+1
if ii == Nxy:
ii = 0
obj.addFace([obj.addVertex(p[i]), obj.addVertex(p[i+Nxy]),
obj.addVertex(p[ii+Nxy]),obj.addVertex(p[ii])])
doc.addObject( obj )
import traceback
import sys
try:
#
drawCylinder(8)
except:
info=sys.exc_info()
p(info[0])
p(info[1])
p(*traceback.extract_tb(info[2]))- -
- -